随机振动rms计算公式,基于随机振动均方根值计算公式的应用概述

你知道吗？在工程领域，随机振动分析可是个高大上的话题。这不，最近我在研究随机振动时，发现了一个超级实用的工具——随机振动rms计算公式。别小看了这个公式，它可是能帮你解决不少难题呢！今天，我就来跟你好好聊聊这个神秘的公式，让你对它有个全面的认识。

什么是随机振动rms计算公式？

首先，得先弄明白什么是随机振动。简单来说，随机振动就是指振动幅度、频率和相位都是随机的振动。而rms，全称是Root Mean Square，中文意思是均方根值，它是一个用来衡量振动强度的指标。

那么，随机振动rms计算公式是什么呢？其实，它就是一个用来计算随机振动均方根值的公式。这个公式可以帮你快速、准确地计算出振动强度，对于工程设计和分析来说，可是非常有用的。

随机振动rms计算公式的由来

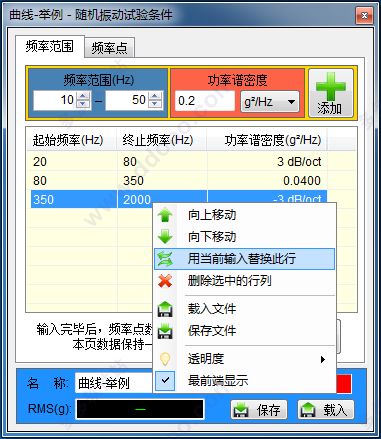
你知道吗？这个公式可是有着悠久的历史呢！早在20世纪初，科学家们就开始研究随机振动了。经过多年的努力，他们终于找到了一个计算随机振动rms的公式。

这个公式最早是由英国物理学家约翰·冯·诺伊曼提出的。后来，经过无数次的改进和完善，这个公式逐渐成为了随机振动分析中的经典公式。

随机振动rms计算公式的应用

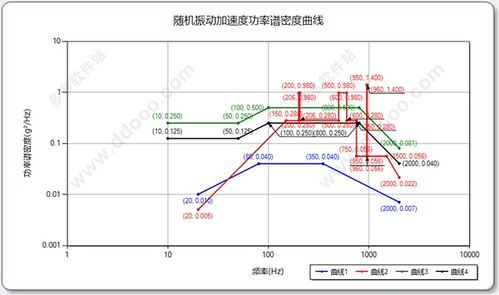
那么，这个公式到底有什么用呢？其实，它的应用范围非常广泛，比如：

1. 机械设计：在机械设计中，随机振动rms计算公式可以帮助工程师评估机械结构的振动强度，从而确保机械的稳定性和可靠性。

2. 汽车工程：在汽车工程领域，这个公式可以用来分析汽车在行驶过程中的振动情况，为汽车设计提供依据。

3. 航空航天：在航空航天领域，随机振动rms计算公式可以帮助工程师评估飞行器的振动强度，确保飞行器的安全性能。

4. 土木工程：在土木工程领域，这个公式可以用来分析桥梁、建筑等结构的振动情况，为工程设计提供参考。

随机振动rms计算公式的计算方法

那么，如何使用这个公式进行计算呢？下面，我就来给你详细介绍一下。

首先，你需要知道随机振动的自谱密度函数S(ω)，它是描述随机振动特性的一个重要参数。根据以下公式计算随机振动rms：

\\[ V_{rms} = \\sqrt{\\frac{1}{T} \\int_{0}^{T} [v(t)]^2 dt} \\]

其中，\\( V_{rms} \\) 是随机振动的均方根值，\\( v(t) \\) 是随机振动的时间历程，\\( T \\) 是时间周期。

如果你对自谱密度函数不太了解，也可以使用以下简化公式：

\\[ V_{rms} = \\sqrt{\\frac{1}{2} \\int_{0}^{\\infty} S(\\omega) d\\omega} \\]

这个公式更加简单易用，但需要注意的是，它只适用于自谱密度函数在无穷远处趋于零的情况。

通过这篇文章，相信你对随机振动rms计算公式有了更深入的了解。这个公式在工程领域有着广泛的应用，对于工程师来说，掌握这个公式无疑是一个巨大的优势。所以，赶快拿起你的计算器，开始研究这个神奇的公式吧！相信它一定会给你带来意想不到的收获。